Introduction
Often represented as mimicking the human brain. A Neuron represents an algorithm. The neuron gets the input data and produces output. The connection between the Neuron are weighted, and organised in layers
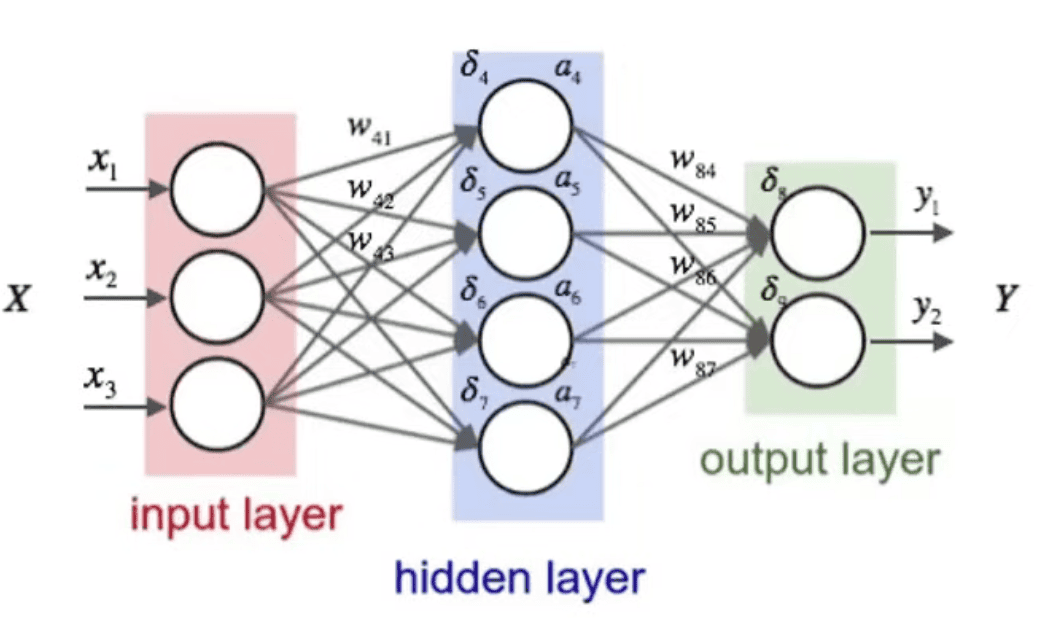
Hidden layers will be multiple, a Neural network with more than 3 or 3 hidden layers is considered to be a Deep Learning Network
FNN - Feed forward Neural Network - The data strictly moves from left to right. It won’t go in cycle (back and forth)
Back Propagation - Move backword on the network and adjusts the weights, why? todo
Loss Function - Finds the error rate by comparing the ground truth and prediction
Neuron’s Algorithm (Activation Functions) - affects the connected outputs, eg RELU
Dense - When the next network layer increases, Sparse otherwise
Deep Learning Algorithms, Not the Activation Function
Supervised
- FNN - Feed-fully Forward Neural Network
- RNN - Recurrent Neural Network
- CNN - Convoluted Neural Network Unsupervised Deep Belief Networks (DBN) Stacked Auto Encoders (SAE) Restricted Boltzmann Machines (RBMs)
Activation Functions
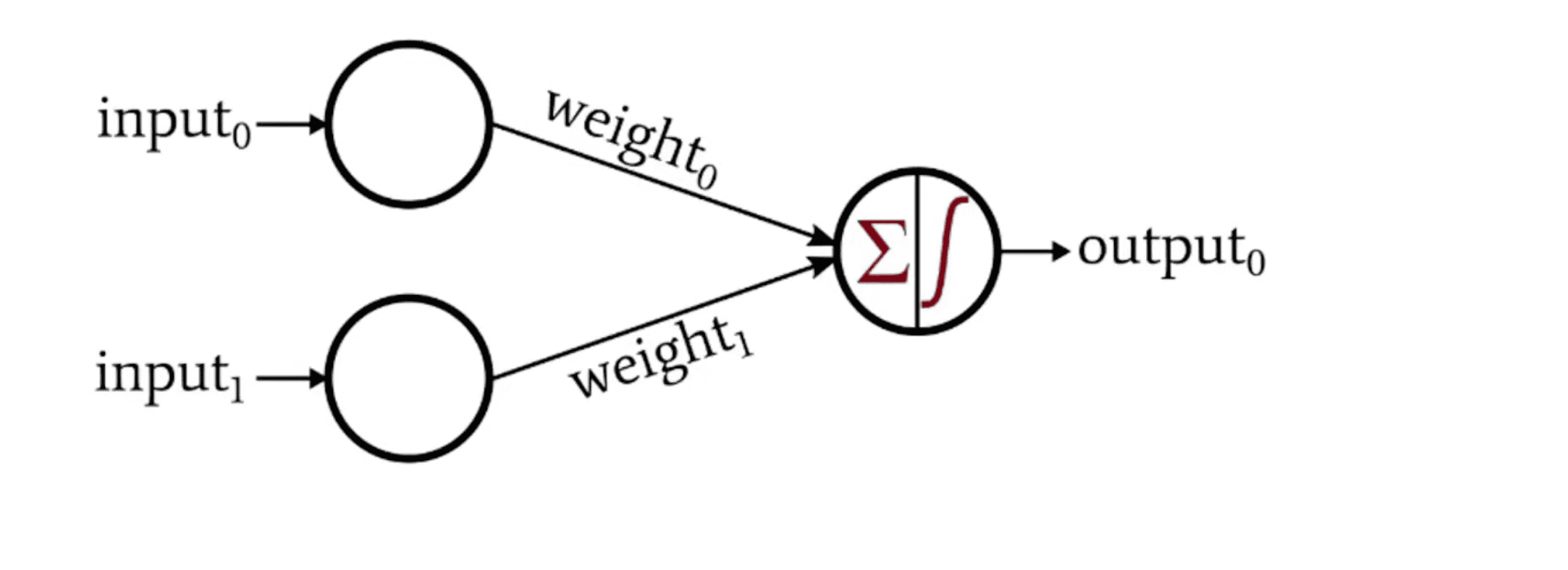
The output of the activation function is in the range of 0 to - 1 or -1 to 1, the name activation function signifies “whether data is going to move forward or not, acts like a gate”
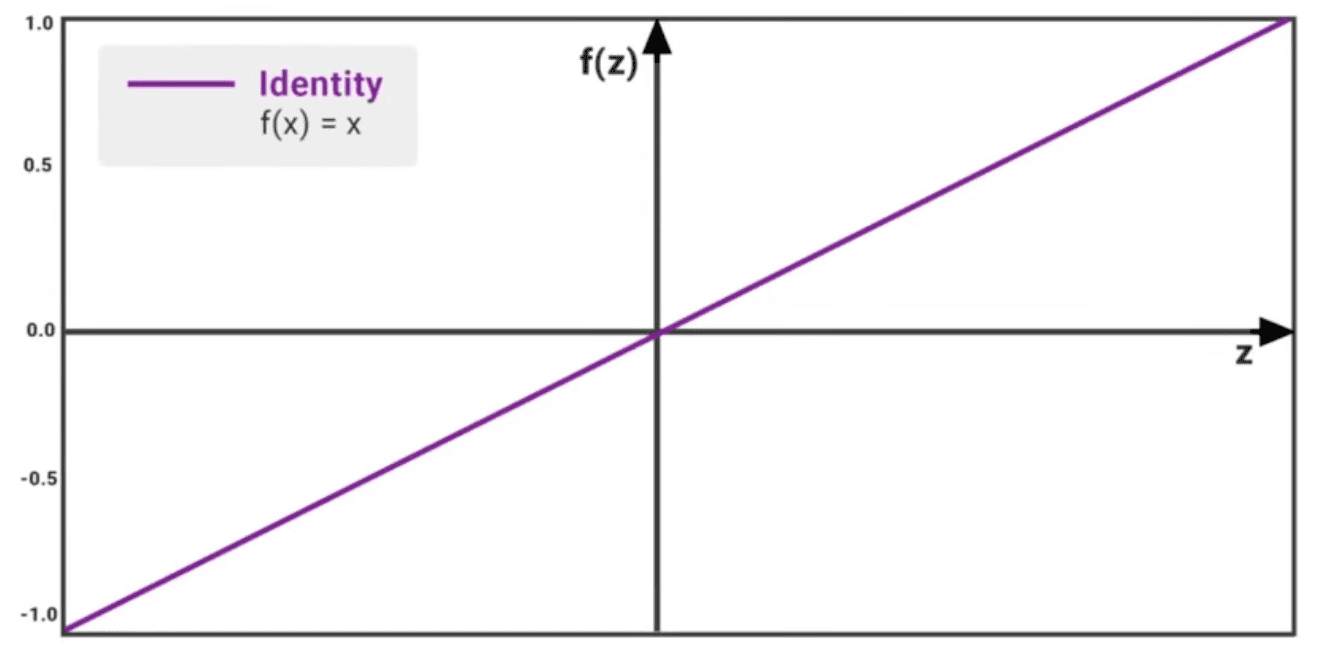
Linear Activation Function - Only pass data forward (also known as Identity function)
- The model is not really learning, doesn’t improve upon error term
- cannot perform back propagation
- cannot have layers, has only one layer
- cannot handle complex non-linear data
- derivative is 1, what you put is what you get
Non linear activation function - Perform back propagations
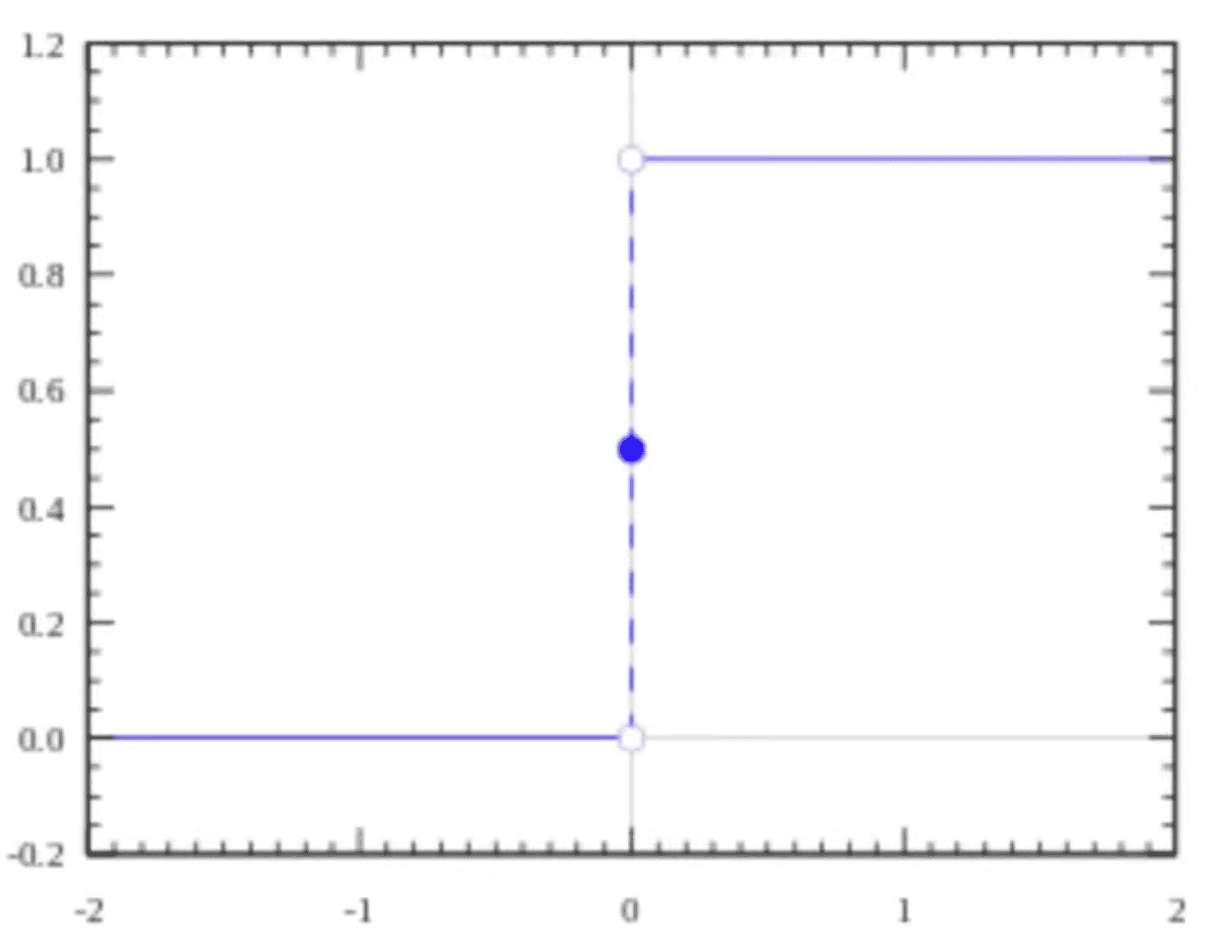
Binary Step - Activate on threshold
- Yes or No, {0, 1}
- Not much used today
Sigmoid - continuous logistic function, squashed between 0 and 1
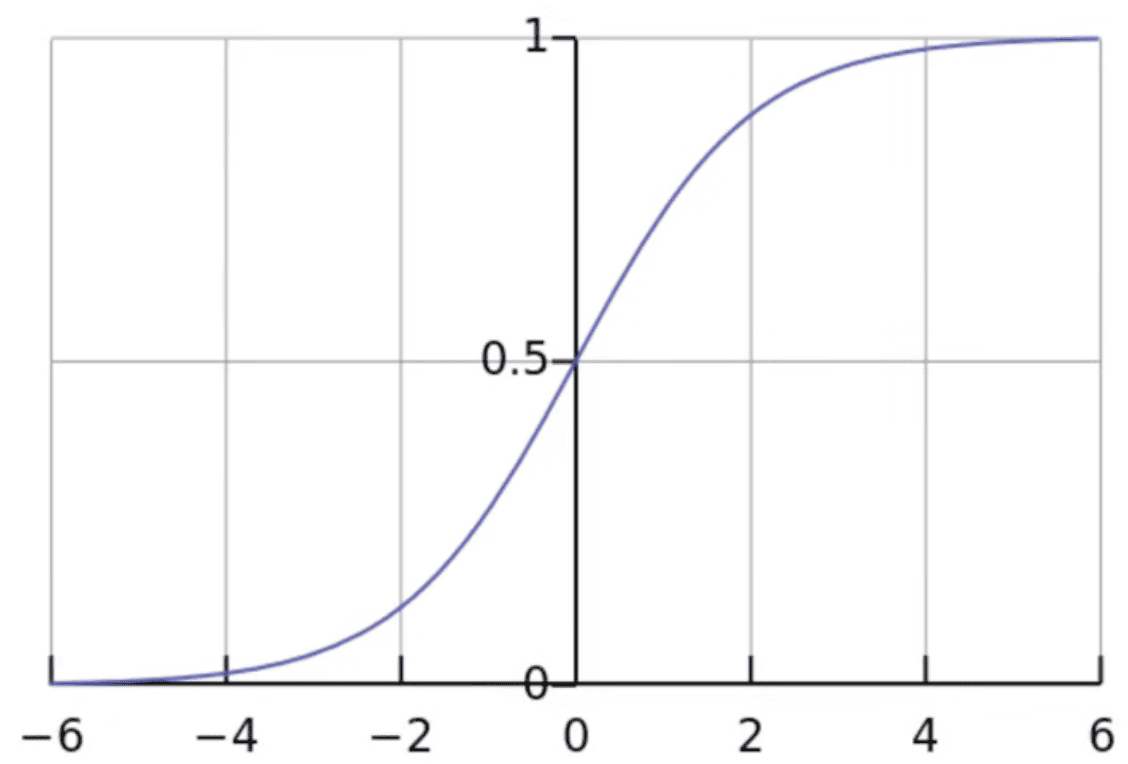
- Logistic curve that represents an S shape
- Handles binary and muliti-classification
- Cat, Dog and Donkey, why not
- One of the most used activation function
- Responds less to x near the end (the vanishing gradient problem, where the network refuses to learn further)
- Range (0,1)
Tanh - scaled version of sigmoid
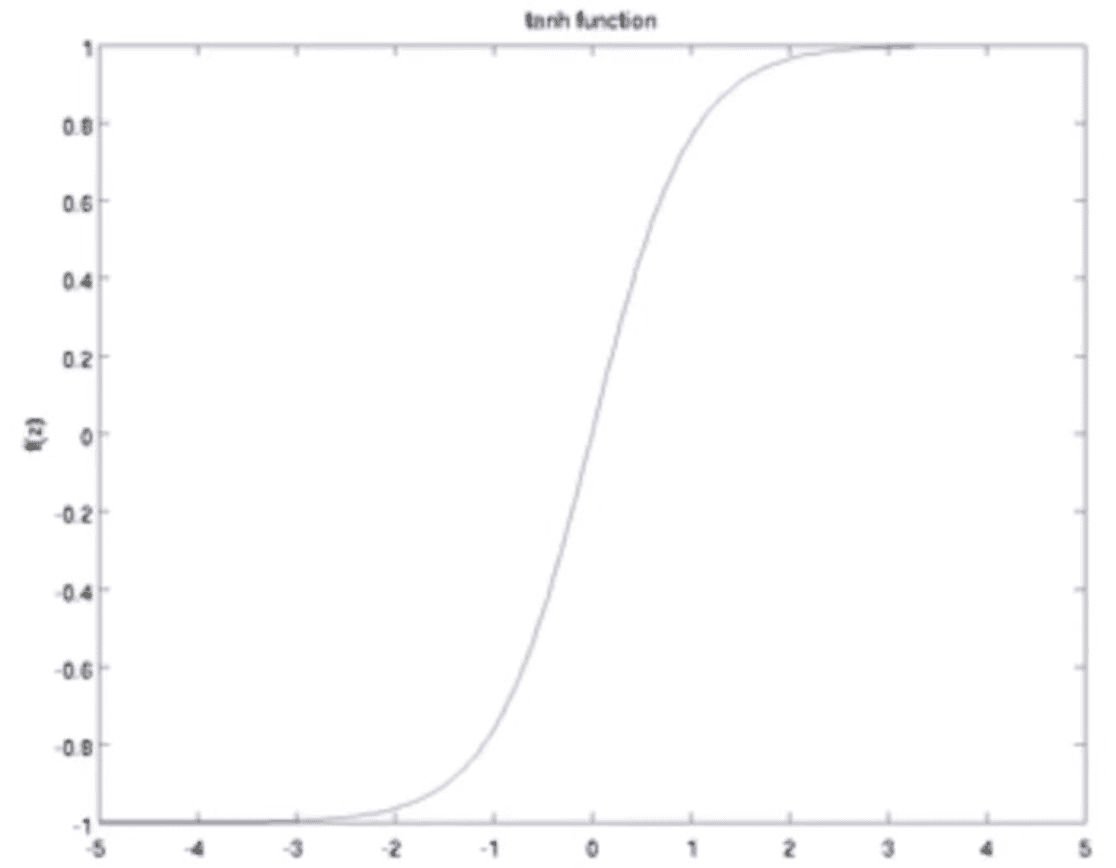- The scale is larger, but still have the vanishing gradient problem
- Sigmoid saturates earlier, where are in Tanh, mean is 0 → better gradients
ReLU - Treats any negative value as 0, (most commonly used functions)
Rectified Linear Unit Activation Function
The positive axis linear, negative axis is always 0
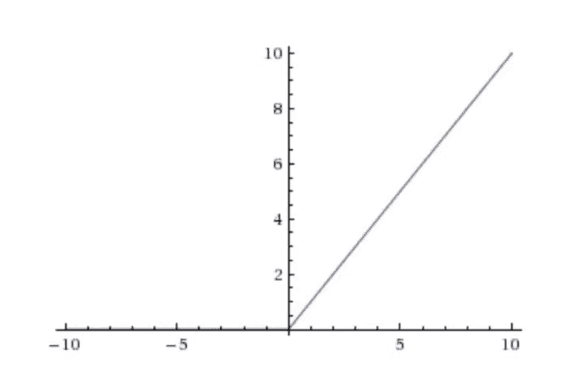
- Range is [0, Infinity)
- ReLU sparsely trigger the neuron, unlike Tanh and Sigmoid where the network become dense, since almost all the neurons fire
- Less costly and more effective
- Negative values often mean “feature not present”
- Dying ReLU: if a neuron keeps getting negative inputs, gradient = 0 → it stops learning
Leaky ReLU - counters dying ReLU problem with a small slope of negative values
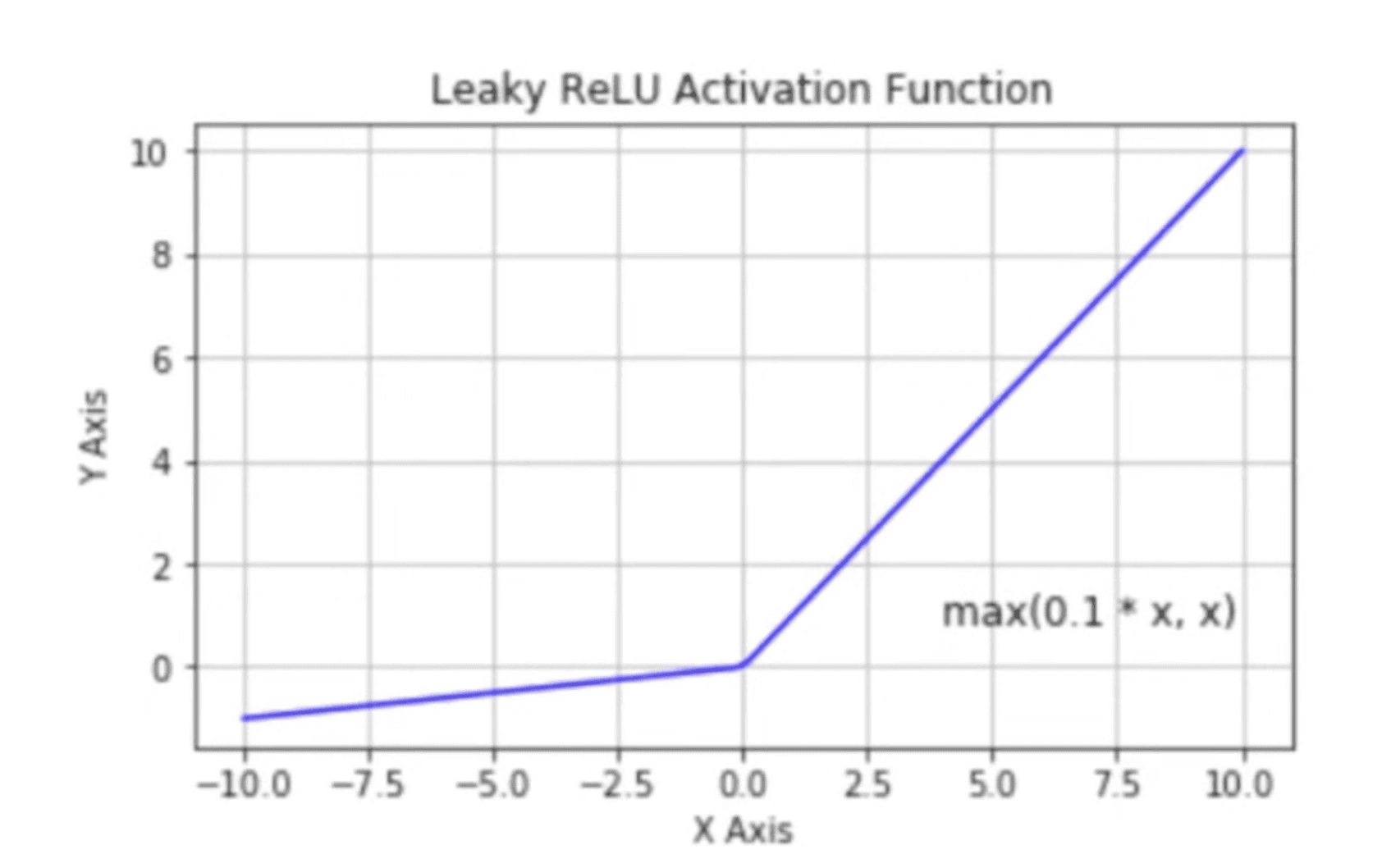
- Reduces the risk of “dying ReLU problem”
- Saves some nodes from death
Parameterised ReLU - Negative slope is fixed at 0.01x
ReLU6 - The upper value have some max value, ie bound
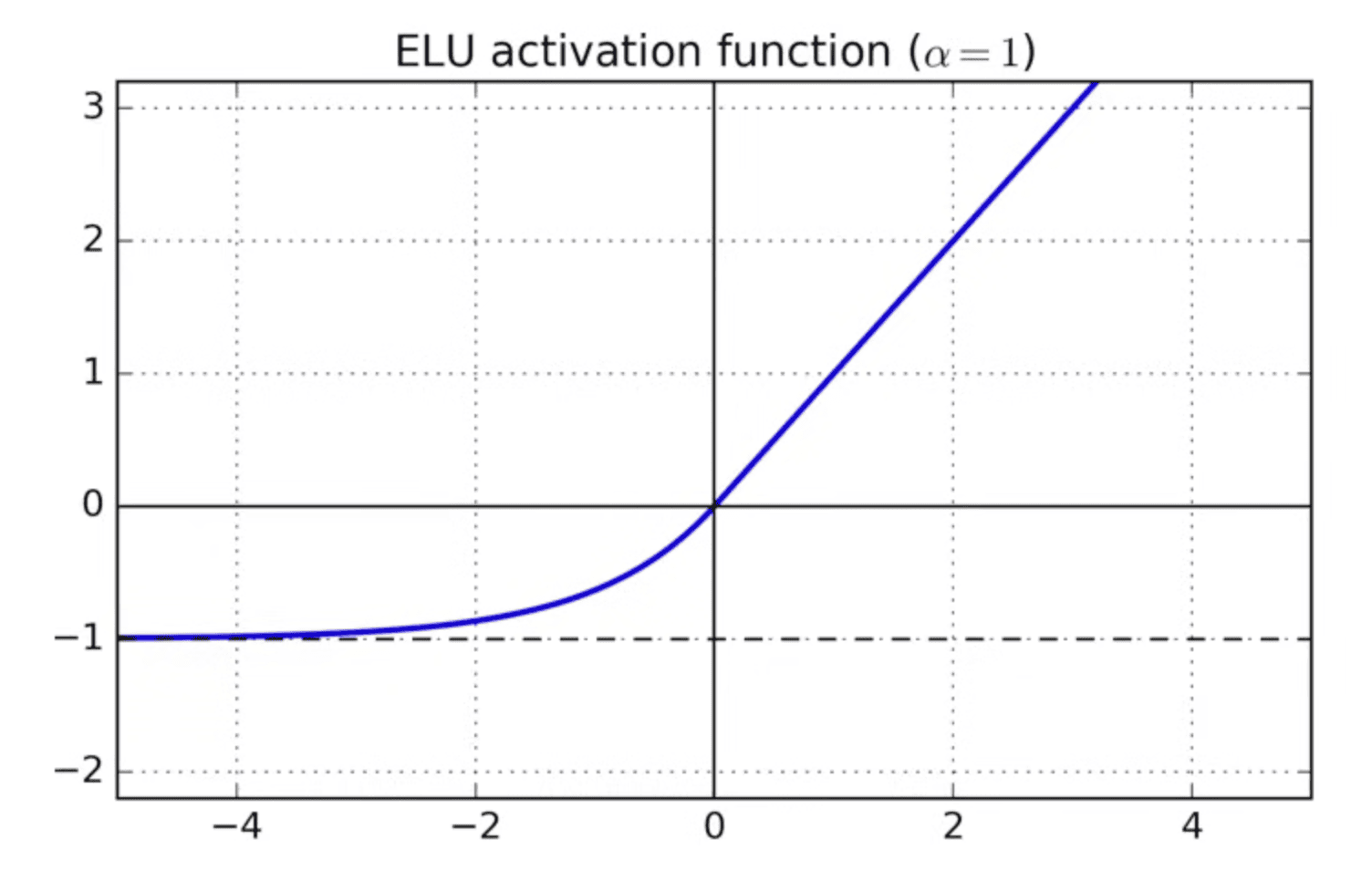
ELU - Exponential Linear Unit
- Linear gradient on the positive axis, has a slope toward -1
- Something between ReLU and Leaky ReLU
- Saturates at larger negative values
Swish activation functions
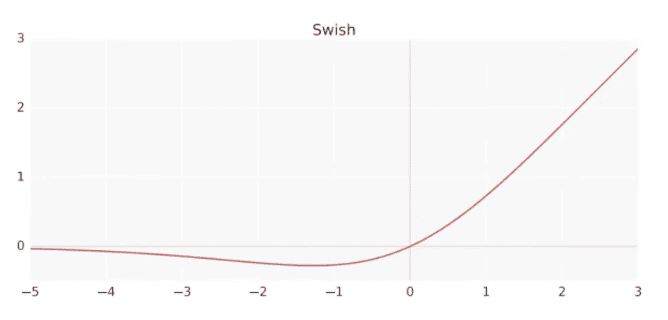Suggested by the Google team as a replacement to ReLU
The idea is Very Negative Values will zero out
Maxout (n)
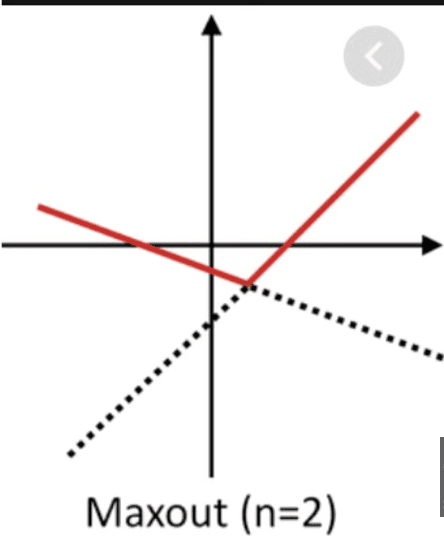Has the benefits of ReLU but doensn’t have the dying ReLU problem. However Maxout is expensive as it doubles the parameters for each neuron?